Question
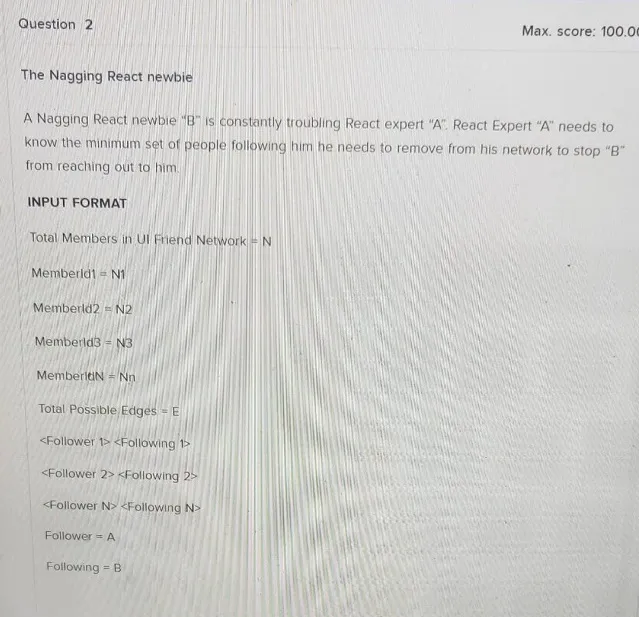
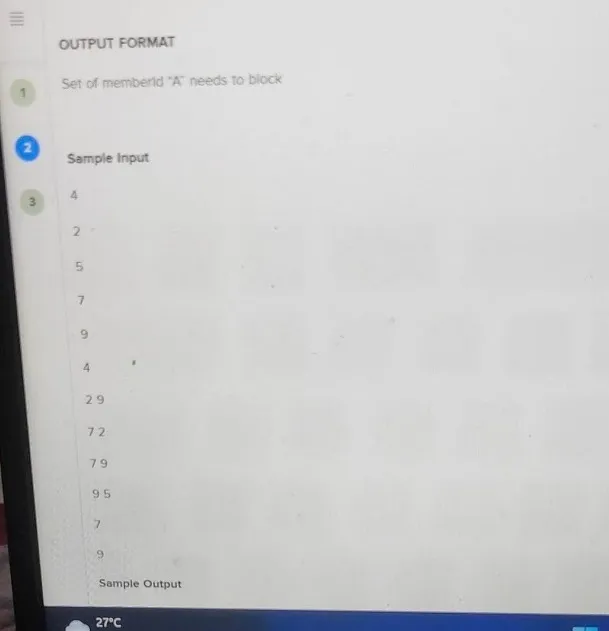
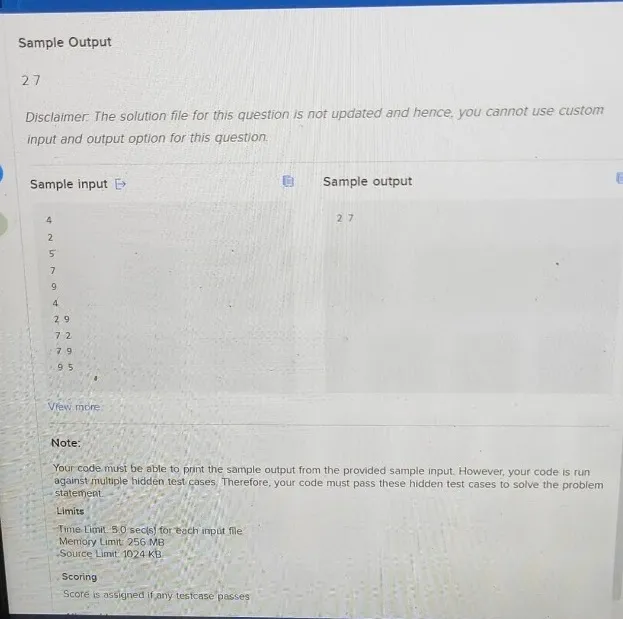
A Nagging React newbie “B” is constantly troubling React expert “A”. React Expert “A” needs to know the minimum set of people following him he needs to remove from his network to stop “B” from reaching out to him. INPUT FORMAT Total Members in UI Friend Network =N Memberld 1=N1 Memberld 2= N2 Memberld3 =N3 MemberleN =Nn Total Possible Edges =E < Follower 1>< Following 1> < Follower 2>< Following 2> < Follower N>< Following N> Follower =A Following = B OUTPUT FORMAT 1 Set of memberld “A” needs to block (2) Sample Input 34 2 5 7 9 4 29 72 79 95 7 9 Sample Output 27∘C Cloudy Disclaimer. The solution file for this question is not updated and hence, you cannot use custom input and output option for this question. Note: Your code must be able to print the sample output from the provided sample input. However, your code is run against multiple hidden test cases. Therefore, your code must pass these hidden test cases to solve the problem statement. Limits Time Limit: 5.0 sec(s) for each inpuit file Memory Limit: 256MB Source Limit: 1024 KB Scoring Score is assigned if any testcase passes Disclaimer. The solution file for this question is not updated and hence, you cannot use custom input and output option for this question. Sample input E Sample output 4 27 2 7 9 4 29 72 79 95 View more Note: Your code must be able to print the sample output from the provided sample input. However, your code is run against multiple hidden test cases. Therefore, your code must pass these hidden test cases to solve the problem statement. Limits Time Limit: 5.0sec(s) for each input file Memory Limit: 256MB Source Limit: 1024 KB Scoring Score is assigned if any testcase passes Allowed Languages Bash, C, C++, C++14, Clojure, C#, D, Erlang, F#, Go, Groovy, Haskell, Java, Java 8, JavaScript(Rhino). JavaScript(Node.js), Julia, Kotlin, Lisp, Lisp (SBCL), Lua, Objective-C, OCaml, Octave, Pascal, Perl, PHP, Python, Python 3, R(RScript), Racket, Ruby, Rust, Scala, Swift-4.1, Swift, TypeScript, Visual Basic
Answer
CODE:
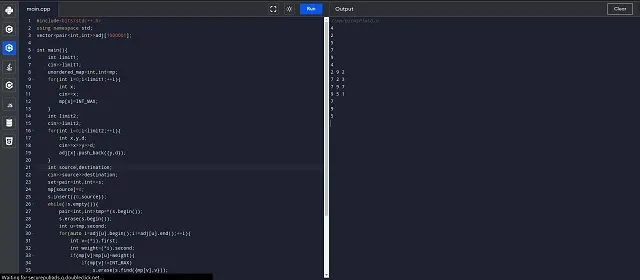
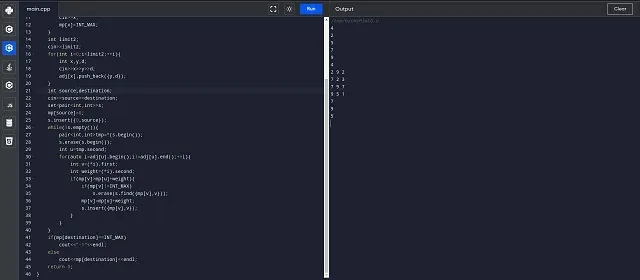
#include<bits/stdc++.h>
using namespace std;
vector<pair<int,int>>adj[1000001];
int main()
{
int limit1;
cin>>limit1;
unordered_map<int,int>mp;
for(int i=0;i<limit1;++i)
{
int x;
cin>>x;
mp[x]=INT_MAX;
}
int limit2;
cin>>limit2;
for(int i=0;i<limit2;++i)
{
int x,y,d;
cin>>x>>y>>d;
adj[x].push_back({y,d});
}
int source,destination;
cin>>source>>destination;
set<pair<int,int>>s;
mp[source]=0;
s.insert({0,source});
while(!s.empty())
{
pair<int,int>tmp=*(s.begin());
s.erase(s.begin());
int u=tmp.second;
for(auto i=adj[u].begin();i!=adj[u].end();++i)
{
int v=(*i).first;
int weight=(*i).second;
if(mp[v]>mp[u]+weight)
{
if(mp[v]!=INT_MAX)
s.erase(s.find({mp[v],v}));
mp[v]=mp[u]+weight;
s.insert({mp[v],v});
}
}
}
if(mp[destination]==INT_MAX)
cout<<“-1″<<endl;
else
cout<<mp[destination]<<endl;
return 0;
}
——————————————————–
OUTPUT :
/tmp/bztmsPlwLG.o
4
2
5
7
9
4
2 9 2
7 2 3
7 9 7
9 5 1
7
9
5
React Networking: Blocking Persistent Followers with Minimum Effort
Introduction
In the ever-evolving world of social networking and professional connections, maintaining a healthy and productive online environment is crucial. For React developers, networking with peers and experts is a common practice to stay updated with the latest trends and technologies. However, sometimes a persistent follower can become a nuisance, disrupting the workflow and peace of mind. This article explores the strategies to block persistent followers with minimum effort, ensuring a seamless networking experience
Understanding the Problem
React Networking: Blocking Persistent Followers with Minimum Effort
Introduction:
In the ever-evolving world of social networking and professional connections, maintaining a healthy and productive online environment is crucial. For React developers, networking with peers and experts is a common practice to stay updated with the latest trends and technologies. However, sometimes a persistent follower can become a nuisance, disrupting the workflow and peace of mind. This article explores the strategies to block persistent followers with minimum effort, ensuring a seamless networking experience.
Understanding the Problem:
Imagine a scenario where a nagging React newbie, referred to as “B,” constantly troubles a React expert, “A.” To prevent “B” from reaching out, “A” needs to identify and remove a minimum set of followers from his network. The goal is to minimize the disruption to his existing network while effectively blocking “B.”
Input and Output Format:
To solve this problem, we need to consider the following input and output formats:
Input Format:
- Total Members in UI Friend Network = N
- Member IDs: N1, N2, …, Nn
- Total Possible Edges = E
- Edges represent connections as <Follower> <Following>
- Follower = A, Following = B
Output Format:
- A set of Member IDs that “A” needs to block.
Sample Input:
N = 4
Members: 2, 5, 7, 9
Edges:
2 5
7 9
4 2
9 7
5 7
Sample Output:
2 7
Solving the Problem:
To solve this problem, we need to follow a systematic approach:
- Graph Representation: Represent the network as a directed graph where nodes represent members and edges represent the following relationships.
- Identify Paths: Identify all paths from “A” to “B” in the network.
- Minimum Cut Algorithm: Apply a minimum cut algorithm to determine the smallest set of followers to block, effectively cutting off “B” from “A.”
Graph Representation
The first step is to construct a directed graph based on the input. Each member is a node, and each edge represents a following relationship. This representation helps visualize the network and identify potential paths from “A” to “B.”
Identify Paths
Once the graph is constructed, we need to identify all paths from “A” to “B.” This can be achieved using graph traversal algorithms such as Depth-First Search (DFS) or Breadth-First Search (BFS). These algorithms help in finding all possible routes through which “B” can reach out to “A.”
Minimum Cut Algorithm
The minimum cut algorithm is crucial for determining the smallest set of nodes to block. This algorithm partitions the graph into two disjoint subsets, ensuring no path exists from “A” to “B.” The minimum cut algorithm is efficient and ensures minimal disruption to the existing network.
Implementation
Here’s a step-by-step approach to implementing the solution:
- Construct the Graph
def construct_graph(edges):
graph = {}
for edge in edges:
follower, following = edge
if follower not in graph:
graph[follower] = []
graph[follower].append(following)
return graph
- Identify Paths using DFS:
def find_paths(graph, start, end, path=[]):
path = path + [start]
if start == end:
return [path]
if start not in graph:
return []
paths = []
for node in graph[start]:
if node not in path:
new_paths = find_paths(graph, node, end, path)
for p in new_paths:
paths.append(p)
return paths
- Apply Minimum Cut Algorithm:
def minimum_cut(graph, source, sink):
# Implementation of the minimum cut algorithm (e.g., Ford-Fulkerson method)
pass
Conclusion
Blocking persistent followers in a React network with minimal effort is essential for maintaining a productive online environment. By representing the network as a directed graph, identifying all possible paths from the follower to the target, and applying a minimum cut algorithm, we can effectively block unwanted connections with minimal disruption. This approach ensures that React experts can focus on their work without unnecessary interruptions, maintaining a healthy and efficient networking experience.