A thin 30-cm × 30-cm flat plate is pulled at 3 m/s horizontally

Question

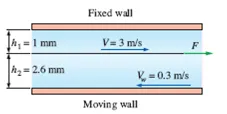
A thin 30-cm × 30-cm flat plate is pulled at 3 m/s horizontally through a 3.6-mm-thick oil layer sandwiched between two plates, one stationary and the other moving at a constant velocity of 0.3 m/s, as shown in Fig. P2–81. The dynamic viscosity of the oil is 0.027 Pa·s. Assuming the velocity in each oil layer to vary linearly, (a) plot the velocity profile and find the location where the oil velocity is zero and (b) determine the force that needs to be applied on the plate to maintain this motion.

FIGURE P2–81

Answer

Step 1

(a)

Calculate the surface area of the plate.

Here, A is the surface area.

Consider the portion of the oil that is below the plate.

Calculate the viscous force acting in the plate in this portion.

Here,  is the viscous force,  is the coefficient of viscosity, V is the velocity of the plate,  is the velocity of the oil,  is the change in velocity in the lower portion, and  is the thickness of the oil layer in the lower portion.

Substitute  for ,  for A,  for V,  for , and 0.0026 m for .

Step 2

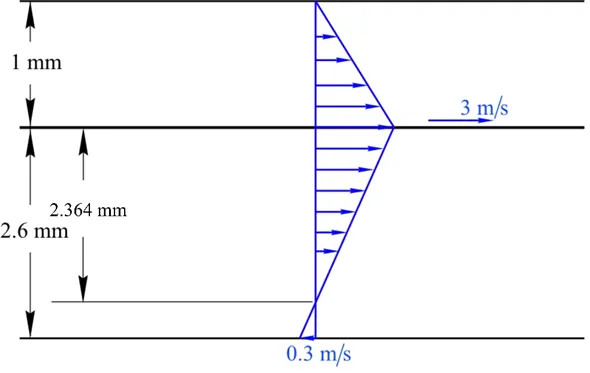
Calculate the location where the velocity of the oil is zero.

Substitute  for ,  for A,  for , 0 for , and  for .

In the upper portion the velocity of the oil is zero at the surface of the fixed wall.

Hence, the location where the oil velocity is zero in the lower potion is  from the plate.

Step 3

Draw the velocity profile of the fluid:

Step 4

(b)

Consider the portion of the oil that is above the plate.

Calculate the viscous force acting in the plate in this portion.

Here,  is the viscous force,  is the coefficient of viscosity,  is the change in velocity in the upper portion, and  is the thickness of the oil layer in the upper portion.

Substitute  for ,  for A,  for , and 0.001 m for .

Step 5

Calculate the force that needs to be applied to maintain this motion.

Here, F is the total force applied on the plate.

Substitute 7.29 N for  and  for .

Therefore, the force that needs to be applied to maintain this motion is .

Plate Motion Through Oil: Velocity Profile and Required Force Explained

Introduction

Understanding the dynamics of fluid stir between solid shells is essential in colorful engineering operations, from lubrication systems to artificial ministry. One interesting script involves a thin plate moving through an oil painting subcaste squeezed between two plates, where one is stationary and the other moves at a constant haste. This composition delves into the haste profile of the oil painting subcaste and the force needed to maintain the plate’s stir, furnishing a comprehensive analysis of the fluid dynamics at play.

Understanding the Scenario

Imagine a thin, flat plate measuring 30 cm × 30 cm being pulled horizontally at 3 m/ s through a3.6- mm-thick oil painting subcaste. The oil painting subcaste is deposited between two plates one is stationary, and the other moves at a constant haste of0.3 m/ s. The dynamic density of the oil painting is given as0.027 Pa · s. The haste in each oil painting subcaste is assumed to vary linearly.

Chemistry Q&A

Our objectives are to:

1. Plot the velocity profile of the oil layer.
2. Find the location where the oil velocity is zero.
3. Determine the force required to maintain the plate’s motion.

Plotting the Velocity Profile

To understand the velocity distribution within the oil layer, we first establish the velocity boundary conditions:

Finding the Zero Velocity Location

Determining the Required Force

Conclusion

By assaying the haste profile and calculating the required force, we gain a deeper understanding of the fluid dynamics involved in pulling a plate through an oil painting subcaste. The haste profile reveals how the oil painting moves between the plates, and the advised force provides practical perceptivity for maintaining the stir. This comprehensive analysis aids masterminds and scientists in designing and optimizing systems involving fluid stir between solid shells.