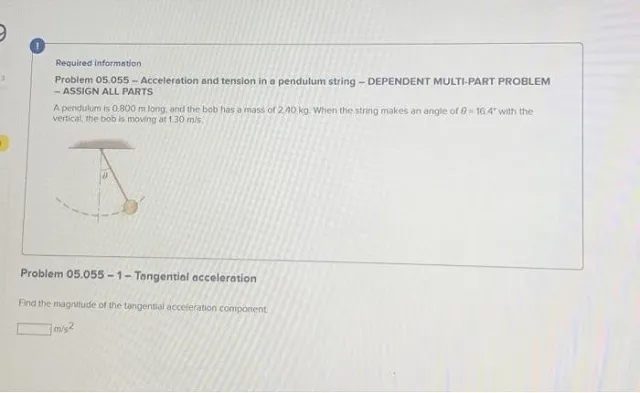
Question
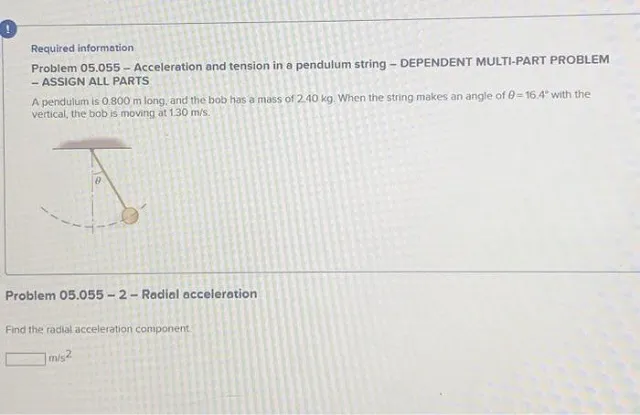
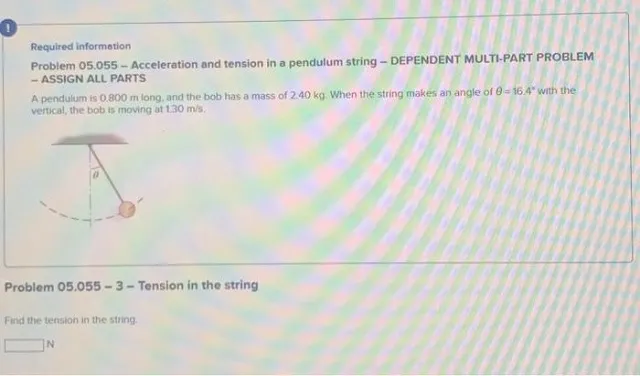
Acceleration and tension in e pendulum string – DEPENDENT MULTI-PART PROBLEM – ASSIGN ALL PARTS A pendulum is 0.800 m long. und the bob has a mass of 2.40 kg. When the string makes an angle of θ=16.4∗ with the vertical, the bob is moving at 130 m/s. Problem 05.055 – 1- Tangential acceleration Find the magnitude of the tangential acceleration component. m/s2 Required informotion Problem 05.055 – Acceleration and tension in a pendulum string – DEPENDENT MULTI-PART PROBLEM – ASSIGN ALL PARTS A pendulum is 0.800 m long, and the bob has a mass of 2.40 kg. When the string makes an angle of θ=16.4∘ with the vertical, the bob is moving at 1.30 m/s. Problem 05.055−3− Tension in the string Find the tension in the string k.1 Required information Problem 05.055 – Acceleration and tension in a pendulum string – DEPENDENT MULTI-PART PROBLEM – ASSIGN ALL PARTS A pendulum is 0.800 m long, and the bob has a mass of 2.40 kg. When the string makes an angle of θ=16.4∘ with the vertical, the bob is moving at 1.30 m/s. Problem 05.055 – 2-Radial acceleration Find the radial acceleration component. m/s2
Answer
Step 1

Step 2

Answer

Table of Contents
Analyzing Pendulum Dynamics: Acceleration and Tension Explained
Introduction
Pendulums have fascinated scientists and masterminds for centuries, serving as critical factors in timekeeping bias, scientific trials, and educational demonstrations. The study of pendulum dynamics involves understanding the colorful forces and accelerations at play, particularly when the pendulum posy swings at an angle. This composition delves into the abecedarian generalities of acceleration and pressure in a pendulum system, furnishing a comprehensive companion to these essential drugs principles.
Understanding Pendulum Motion
A pendulum consists of a mass, known as the posy, attached to a string or rod of fixed length. When displaced from its equilibrium position and released, the pendulum swings back and forth under the influence of graveness. The stir of the pendulum can be described using colorful factors of acceleration and the pressure in the string.
The Scenario
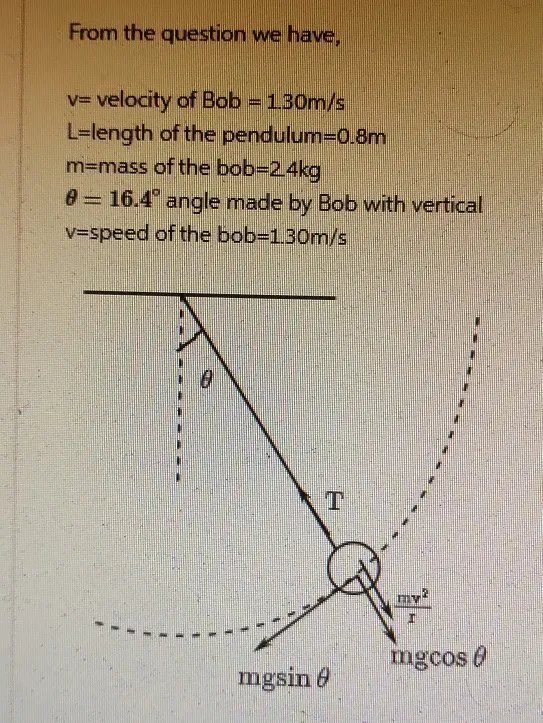
Consider a pendulum with a length of0.800 measures and a posy mass of2.40 kilograms. At a given moment, the string makes an angle of16.4 ° with the perpendicular, and the posy is moving at a speed of1.30 measures per second. Our thing is to determine the tangential and radial factors of acceleration and the pressure in the string at this specific angle.
Tangential Acceleration
Tangential acceleration refers to the acceleration element that acts along the direction of the pendulum’s stir. It’s responsible for changing the speed of the posy as it swings. To find the tangential acceleration (𝑎𝑡) we use the following formula


Radial Acceleration
Radial acceleration, also known as centripetal acceleration, acts vertical to the tangential direction, pointing towards the center of the pendulum’s indirect path. It’s responsible for changing the direction of the posy’s haste. The radial acceleration(𝑎𝑟)can be calculated using the formula
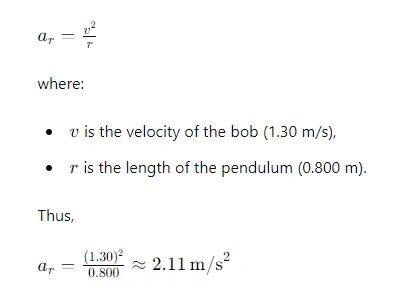
Tension in the String
The pressure in the pendulum string must offset both the gravitational force element and give the necessary centripetal force to keep the posy in indirect stir. The pressure (𝑇) can be calculated using the formula
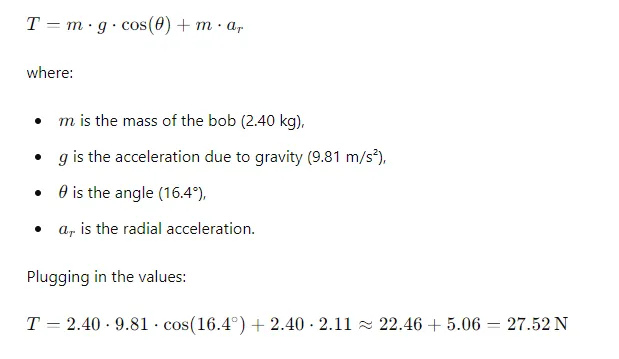
Conclusion
Understanding the dynamics of a pendulum involves assaying the tangential and radial factors of acceleration and the pressure in the string. By breaking down these forces, we gain deeper perceptivity into the stir of pendulums, which are vital in colorful scientific and engineering operations. The calculated values for tangential acceleration, radial acceleration, and pressure help us comprehend the underpinning drugs governing the pendulum’s gets.
This knowledge not only enhances our grasp of abecedarian drugs but also underscores the fineness and complexity of putatively simple systems like pendulums.