In a World Cup soccer match, Juan is running due north toward the goal

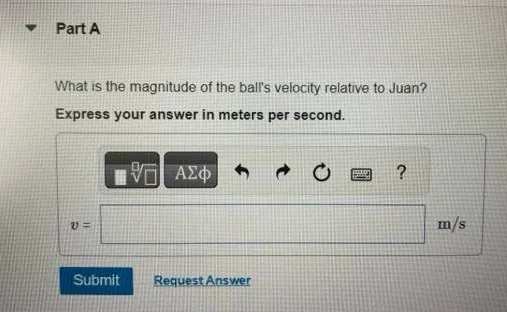
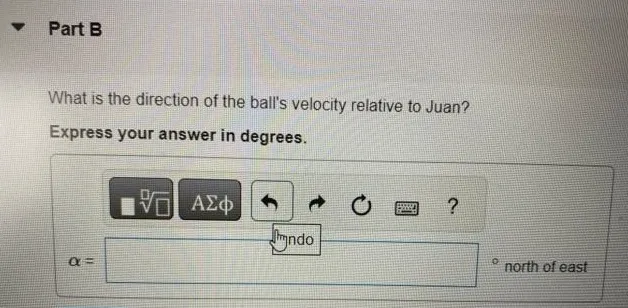
Question

In a World Cup soccer match, Juan is running due north toward the goal with a speed of 7.10 m/s relative to the ground. A teammate passes the ball to him. The ball has a speed of 14.0 m/s and is moving in a direction of 33.4∘ east of north, relative to the ground. What is the magnitude of the ball’s velocity relative to Juan? Express your answer in meters per second. What is the direction of the ball’s velocity relative to Juan? Express your answer in degrees.

Answer

Step 1

Explanation:

Write the velocities in unit vector form

Take x axis to be along East and y axis along North, then the velocity of Juan is v→J=7.1j^ m/s.

The velocity of ball is v→b=14(sin⁡33.40i^+cos⁡33.40j^)=(7.71i^+11.69j^) m/s.

Step 2

Explanation:

Now find the velocity of ball relative to Juan

The velocity of ball relative to Juan can be found using

Step 3

Explanation:

Using the above velocity, find the magnitude and direction

A: The magnitude of ball’s velocity relative to Juan is computed as under:-

vb/J=7.712+4.592vb/J=8.97 m/s

B: The direction angle (North of East) of ball’s velocity relative to Juan is computed as under:-

Answer

A: The magnitude of ball’s velocity relative to Juan is vb/J=8.97 m/s

B: The direction angle (North of East) of ball’s velocity relative to Juan is

• A: The magnitude of ball’s velocity relative to Juan is vb/J=8.97 m/sB: The direction angle (North of East) of ball’s velocity relative to Juan is 𝛼=30.770

How to Calculate Velocity: Step-by-Step Instructions

Understanding how to calculate velocity is fundamental in physics and essential for solving a variety of real-world problems. Velocity, a vector quantity, not only describes the speed of an object but also its direction of motion. This article provides step-by-step instructions on how to calculate velocity, ensuring you grasp both the basic and advanced concepts.

What’s Velocity?

Velocity is defined as the rate at which an object changes its position. Unlike speed, which is a scalar quantity and only considers magnitude, velocity includes both magnitude and direction. The standard unit for velocity is meters per second (m/s).

Introductory Formula for Velocity

The basic formula to calculate velocity is:

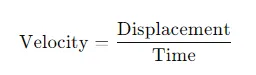
Here, displacement refers to the change in position of the object and is a vector quantity, while time is the duration over which the change occurs.

Step-by-Step Instructions to Calculate Velocity

Step 1: Determine Displacement

Displacement is the straight-line distance between the starting and ending points of an object’s motion. It is important to note the direction of the displacement to ensure accurate velocity calculation.

Example: If a car travels 100 meters east from its starting point, its displacement is 100 meters east.

Step 2: Measure the Time Interval

Measure the time it takes for the object to cover the displacement. This is usually given in seconds (s).

Example: If the car takes 5 seconds to travel 100 meters east, the time interval is 5 seconds.

Step 3: Apply the Velocity Formula

Use the displacement and time values in the velocity formula.

Thus, the velocity of the car is 20 meters per second east.

Calculating Average Velocity

Average velocity is useful when an object’s motion involves changes in speed or direction. The formula for average velocity is:

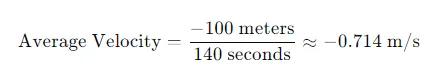
Example:

1. A runner travels 300 meters north in 60 seconds, then 400 meters south in 80 seconds.
2. Total displacement: 300 meters north−400 meters south=−100 meters300 meters north−400 meters south=−100 meters (or 100 meters south).
3. Total time: 60 seconds+80 seconds=140 seconds60 seconds+80 seconds=140 seconds.

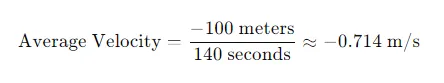
The negative sign indicates the direction is south.

Instantaneous Velocity

Instantaneous velocity is the velocity of an object at a specific moment in time. It is typically determined using calculus, as it involves finding the derivative of the position function with respect to time.

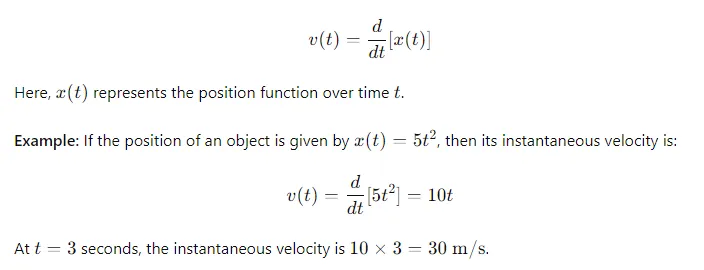
Practical Applications of Velocity

1. Transportation: Calculating the velocity of vehicles helps in planning travel routes and schedules.
2. Sports: Understanding athletes’ velocities aids in performance analysis and strategy development.
3. Engineering: Engineers use velocity calculations in designing and testing machines, ensuring they operate efficiently and safely.
4. Space Exploration: Calculating the velocity of spacecraft is crucial for navigation and mission success.

Conclusion

Calculating velocity is a fundamental skill in physics that has practical applications across various fields. By understanding how to determine displacement, measure time intervals, and apply the velocity formula, you can accurately calculate both average and instantaneous velocities. Mastering these concepts not only enhances your problem-solving abilities but also deepens your understanding of motion and its principles.