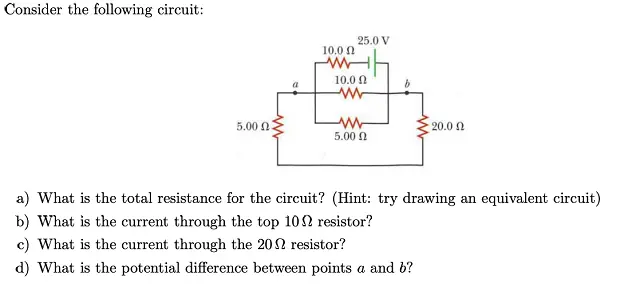
Question
Consider the following circuit: a) What is the total resistance for the circuit? (Hint: try drawing an equivalent circuit) b) What is the current through the top 10Ω resistor? c) What is the current through the 20Ω resistor? d) What is the potential difference between points a and b ?
Answer
Step 1
First, draw the equivalent circuit.
Explanation:
B is the point at the +ve terminal of the battery. A is connected to the negative terminal through a 10Ω resistance. All other resistances are parallel between A and B

Step 2
The 20 and 5 Ohm resistances in series can be considered as a 25 Ohm resistance.
So we have 25,10 and 5 in parallel. Their equivalent resistance will be 1R=15+110+125=1750
R=5017
The other 10 Ohm resistance is in series with this. So total resistance =

Step 3
The 10 Ohm resistance is in series with the batter so the current flowing through it will be equal to the total current in the circuit.

Step 4
The 20 Ohm resistor is in series with the 5. So the path has a resistance of 25 Ohm.
For finding the current we can use the current divider rule.
I=125/(125+110+15)=125/(1750)=217
The current through the 20Ω resistance will be

Step 5
The potential difference between A and B = The equivalent resistance across them × the current in the circuit
V=5017×1.93=5.68
The potential difference between A and B is 5.68 volts

Answer
The circuit can be simplified by considering equivalent parallel and series resistances
Table of Contents
Physics of Circuits: Key Principles and Applications
Electric circuits are foundational to understanding both practical and theoretical aspects of drugs. Whether you are a pupil probing into the subject for the first time or an advanced learner looking to consolidate your knowledge, grasping the crucial principles and operations of circuits is essential. In this composition, we’ll explore the abecedarian generalities of circuit drugs and punctuate their real- world operations.
Key Principles of Electric Circuits
Ohm’s Law
Ohm’s Law is the foundation of circuit analysis. It states that the current( I) flowing through a captain between two points is directly commensurable to the voltage( V) across the two points and equally commensurable to the resistance( R). The formula is
V=IR
This relationship is pivotal for calculating the current, voltage, and resistance in any electrical circuit.
Kirchhoff’s Laws
Kirchhoff’s Laws are vital for assaying complex circuits
- Kirchhoff’s Current Law( KCL): The total current entering a junction equals the total current leaving the junction. This is grounded on the principle of charge conservation.
- Kirchhoff’s Voltage Law( KVL): The sum of all electrical implicit differences around a circle is zero. This is deduced from the principle of energy conservation.
Series and resembling Circuits
- Series Circuits: Components are connected end- to- end, furnishing a single path for current inflow. The total resistance is the sum of individual resistances, and the current is the same through all factors.
- resembling Circuits: factors are connected across common points, furnishing multiple paths for current inflow. The total resistance is set up using the complementary formula
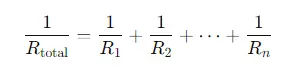
Voltage across each element is the same
Capacitance and Inductance
- Capacitors: store energy in an electric field and are characterized by their capacitance( C). The relationship between the charge( Q), voltage( V), and capacitance is
Q=CV
- Inductors: store energy in a glamorous field and are characterized by their inductance( L). The convinced voltage( V) in an inductor is commensurable to the rate of change of current( I)
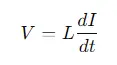
Operations of Electric Circuits
Operations of Electric Circuits
Ultramodern electronic bias, from smartphones to computers, calculate heavily on complex circuits. Integrated circuits( ICs), which contain thousands of bitsy transistors, are the structure blocks of these bias.
Power Distribution
Electrical power distribution systems use circuits to deliver electricity from power shops to homes and businesses. Understanding circuit principles helps in designing effective and safe power grids.
Communication Systems
Circuits are abecedarian in communication technologies, including radios, boxes, and internet structure. Signal processing and transmission are grounded on circuit proposition.
Medical Equipment
Medical bias, similar as MRI machines, ECG observers, and leaders, use sophisticated circuits to serve directly. Knowledge of circuit drugs is pivotal in developing and maintaining these life- saving tools.
Automotive Industry
Modern vehicles are equipped with multitudinous electronic circuits that control everything from machine functions to infotainment systems. Electric and cold-blooded vehicles, in particular, depend on advanced circuit designs.
Renewable Energy Systems
Solar panels, wind turbines, and other renewable energy technologies use circuits to convert, store, and distribute energy. Effective circuit design is crucial to maximizing energy affair and integration with being power grids.
Conclusion
The drugs of circuits encompasses a wide range of principles that are abecedarian to both theoretical studies and practical operations. From Ohm’s Law to Kirchhoff’s Laws, understanding these generalities is essential for assaying and designing electric circuits. The operations of circuits are vast, impacting colorful diligence and aspects of diurnal life. Whether it’s in electronic bias, power distribution, communication systems, medical outfit, automotive technology, or renewable energy, the principles of circuit drugs play a pivotal part.
By learning the crucial principles and exploring their operations, drugs scholars can gain a deeper appreciation of how electric circuits shape the ultramodern world.