Question
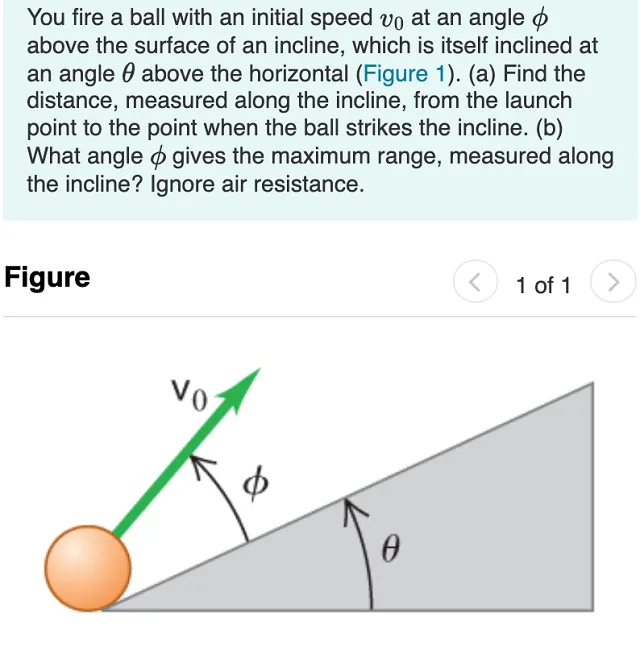
You fire a ball with an initial speed vo at an angle o above the surface of an incline, which is itself inclined at an angle 0 above the horizontal (Figure 1). (a) Find the distance, measured along the incline, from the launch point to the point when the ball strikes the incline. (b) What angle o gives the maximum range, measured along the incline? Ignore air resistance.
Answer
Step 1
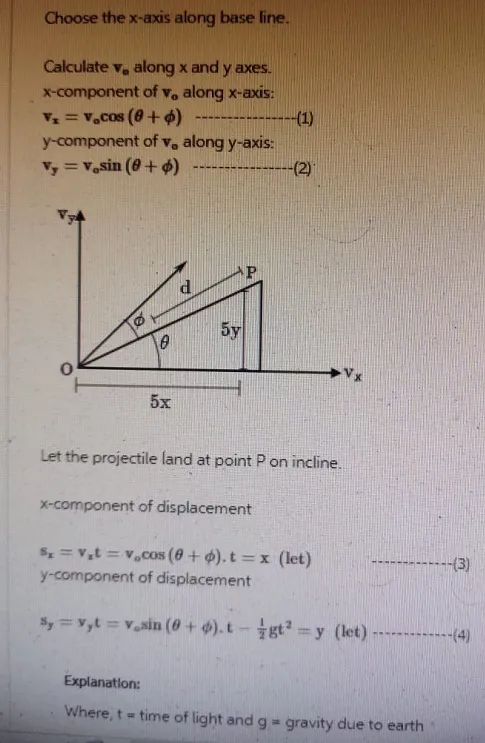
Step 2

Step 3
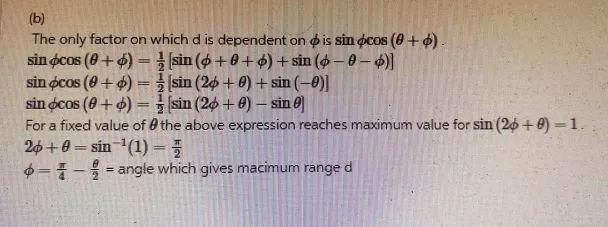
Answer
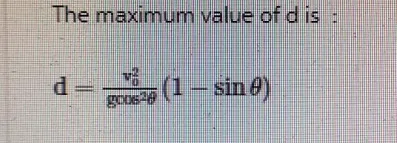
Optimizing Projectile Motion: Finding Distance and Angle for Incline Strikes
Introduction
Projectile motion, a fundamental concept in physics, governs the motion of objects launched into the air under the influence of gravity. While the principles of projectile motion are well-understood in flat, horizontal scenarios, the dynamics change when dealing with inclined surfaces. Inclined surfaces, such as ramps or hills, introduce additional complexities that require a deeper understanding of physics and mathematics to optimize projectile motion effectively. In this comprehensive guide, we will delve into the intricacies of projectile motion on inclined surfaces, focusing on how to optimize the distance and angle for strikes on inclines. By exploring the underlying principles, equations, and strategies, we aim to provide a thorough understanding of this fascinating phenomenon.
The Fundamentals of Projectile Motion on Incline
Projectile motion on an incline involves the interplay of various forces and vectors. When a projectile is launched at an angle above an inclined surface, it experiences both horizontal and vertical components of motion. The gravitational force acts vertically downward, while the incline exerts a normal force perpendicular to its surface. By decomposing the motion into horizontal and vertical components, we can analyze the trajectory of the projectile and calculate its behavior with respect to the incline.
Finding Distance Along the Incline
(a) To determine the distance traveled along the incline from the launch point to the point where the projectile strikes the incline, we employ principles of kinematics and trigonometry. By considering the horizontal and vertical components of motion separately, we can calculate the time of flight and the horizontal displacement. The horizontal displacement, measured along the incline, provides the distance traveled by the projectile before striking the incline. This calculation is essential for understanding the spatial dynamics of projectile motion on inclined surfaces.
Optimizing Angle for Maximum Range
(b) Achieving maximum range along the incline requires careful consideration of the launch angle. By optimizing the launch angle, we aim to maximize the horizontal displacement of the projectile. To find the optimal launch angle, we analyze the trajectory of the projectile and derive an expression that balances the effects of gravity and the incline angle. This angle ensures that the projectile covers the maximum distance along the incline before landing, thus optimizing the effectiveness of the strike.
Ignoring Air Resistance for Simplification
In our analysis, we simplify the scenario by neglecting the effects of air resistance. While air resistance can significantly affect the trajectory of a projectile in real-world scenarios, ignoring it allows us to focus exclusively on the fundamental principles of projectile motion on inclined surfaces. By isolating the effects of gravity and the incline angle, we can gain a deeper understanding of the underlying dynamics without the added complexity of air resistance.
Conclusion
Mastering projectile motion on inclined surfaces requires a combination of physics principles, mathematical techniques, and critical thinking skills. By understanding the fundamentals of projectile motion and applying them to inclined scenarios, we can optimize the distance and angle for strikes on inclines effectively. This comprehensive guide has provided insights into the complexities of projectile motion on inclined surfaces, from calculating distance along the incline to optimizing the launch angle for maximum range. By mastering these concepts, students and enthusiasts alike can enhance their understanding of projectile motion and its applications in various scientific and practical contexts.