Compound A decomposes according to the equation A(e)=2 B( g)+C(e) A sealed

Question

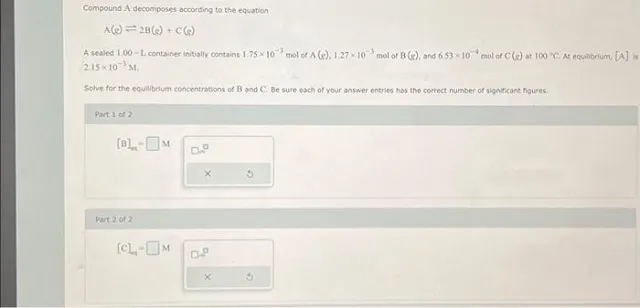
Compound A decomposes according to the equation A(e)=2 B( g)+C(e) A sealed 1.00−L container initially contains 1.75×10−3 mol of A(g),1.27×10−3 mol of B (s), and 6.53×10−4 mol of C(s) at 100×C,At equabrium, [A] is 2,15×10−3MI. Solve for the equabrium concentrations of B and C: Be sure each of your answer entries has the correct number of significant figures; Part 1 of 2 Part2012 [C]s​=M

Answer

Step 1

Step 2

Answer

Calculating Equilibrium: Concentrations of B and C from Compound A Decomposition

Introduction

Chemical equilibrium is a abecedarian conception in chemistry that describes the state in which the rates of the forward and rear responses are equal, leading to constant attention of reactants and products. Understanding how to calculate equilibrium attention is pivotal for prognosticating the geste
of chemical systems. In this composition, we will explore the corruption of emulsion A and determine the equilibrium attention of products B and C. This step- by- step companion will help you grasp the principles of equilibrium and apply them to break real- world chemical problems.

Equilibrium problems are not just academic exercises; they have practical implications in various fields such as pharmaceuticals, environmental science, and industrial chemistry. For instance, in industrial processes, controlling the equilibrium conditions can optimize the yield of desired products, thus making the process more cost-effective and efficient. In environmental science, understanding equilibrium can help in predicting the behavior of pollutants and their impact on ecosystems.

Furthermore, mastering equilibrium concepts is essential for advancing in chemistry education and research. These principles are foundational for more advanced topics in physical chemistry, thermodynamics, and reaction kinetics. They also play a critical role in experimental design and data interpretation, allowing chemists to manipulate conditions to favor certain reactions or products. By delving into the specific case of Compound A’s decomposition, we can build a robust framework for tackling a wide range of equilibrium problems.

Understanding the Reaction

The decomposition of Compound A is represented by the equation:

A(g)⇌2B(g)+C(g)

In this reaction, one mole of gaseous A decomposes into two moles of gaseous B and one mole of gaseous C. The system is initially in a sealed 1.00-L container, and we are given the initial moles of each substance as well as the equilibrium concentration of A.

Given Data and Initial Conditions

Step-by-Step Calculation

Initial Concentrations: Convert the initial moles of each substance to concentrations (M) using the volume of the container:

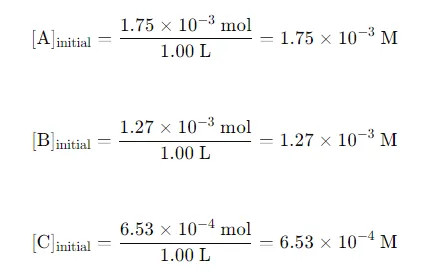
Changes in Concentration: Define the change in concentration of A(g) during the reaction as xxx. Since A decomposes into B and C, the changes can be expressed as:

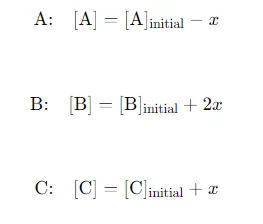
Equilibrium Concentration: At equilibrium, the concentration of A(g) is given as 2.15×10−3 M2.15 \times 10^{-3} \text{ M}2.15×10−3 M. Set up the equation:

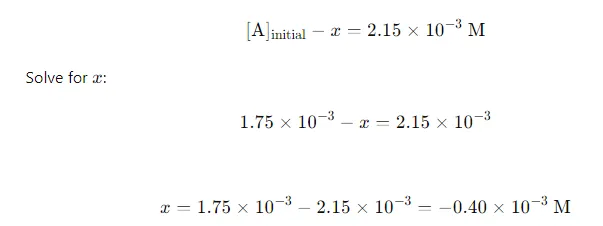
Calculate Equilibrium Concentrations of B and C: Substitute xxx into the expressions for [B] and [C]:

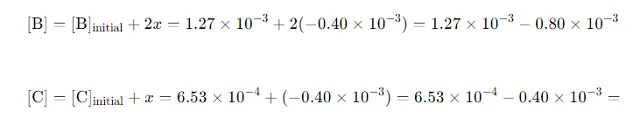
Conclusion

Solving equilibrium problems, such as the decomposition of Compound A at high temperatures, requires a systematic approach and a deep understanding of equilibrium principles. Through careful analysis and mathematical manipulation, we can unravel the complex interplay of reactants and products in chemical systems and predict their behavior under specific conditions. Equilibrium problems not only serve as a valuable tool for honing problem-solving skills but also offer insights into the fundamental principles governing chemical reactions.

By mastering the techniques of equilibrium analysis, students and researchers alike can tackle a wide range of real-world challenges, from designing efficient chemical processes to optimizing reaction conditions for maximum yield. Equilibrium problems provide a bridge between theoretical knowledge and practical applications, fostering a deeper appreciation for the dynamic nature of chemical systems and their role in shaping the world around us. As we continue to explore and apply equilibrium concepts, we contribute to the advancement of science and technology, paving the way for innovation and discovery in the field of chemistry.

Moreover, understanding and applying these principles can have significant environmental and economic impacts. For instance, optimizing reactions to achieve equilibrium more efficiently can lead to reduced energy consumption and lower production costs in industrial settings. In environmental contexts, predicting the equilibrium concentrations of various substances can help in developing strategies to mitigate pollution and its effects on natural ecosystems.

Finally, proficiency in equilibrium calculations is a critical skill for aspiring chemists and professionals in related fields. It equips them with the tools needed to conduct rigorous research, develop new technologies, and contribute to advancements in medicine, energy, and materials science. As we continue to face global challenges, such as climate change and resource scarcity, the ability to understand and manipulate chemical equilibria will be instrumental in developing sustainable solutions. By mastering these concepts, we not only advance our knowledge but also contribute to a more sustainable and scientifically informed future.